.

. 昆明理工大学试卷（历年试题）

考试科目： 概率统计B(48学时) 考试日期： 命题教师：

2013年概率统计试题

一、填空题（每小题4分，共40分）

1.设A,B,C 为三个事件，则A,B,C 中至少有两个发生可表示为 。

2.已知1()4p A =，1(|)2p A B =，1(|)3

p B A =，则()p A B ?= 。 3.设事件A,B 互不相容，且1()2p A =，1()3

p B =，则()p AB = 。 4．进行独立重复实验，设每次成功的概率为p ,失败的概率为1p -,将实验进行到出

现一次成功为止，以X 表示实验次数，则()p X k == 。

5．已知随机变量X 服从参数2λ=的泊松分布，即(2)X P :，则(0)p X == 。

6．已知随机变量(2,1)X N -:，(2,1)Y N :且,X Y 相互独立，则2X Y -服从的分布

是 。

7．若随机变量X 满足()1,()2,E X D X =-=则2(31)E X -= 。

8．设12,X X 是来自于总体X 的样本，1121233X X μ=+)，2121122

X X μ=+)为总体均值μ的无偏估计，则12,μμ))中较有效的是 。

9．设12,,n X X X L 为来自总体2(,)N μσ的一个样本，2σ已知，则

212()

n i i X

X σ=-∑服从的分布是 ，2

12()n i i X μσ=-∑服从的分布是 。

10．设12,,n X X X L 为来自总体2(,)N μσ的一个样本，2σ未知，则μ的1α-的置信区

间是为 。

一、 填空题（每小题4分，共40分）

1．AB BC AC U U 2. 13 3.12

4. ()p X k ==1(1)k p p -- 1,2,k =L

5. 2e -

6.(6,5)N -

7. 8

8. 2μ)

9. 22(1),

()n n χχ-

.

.

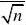
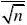
10. 22(_(1),(1))x n x n αα-- 二、(10分)某保险公司把被保险人分为三类：谨慎的、一般的、冒失的，统计资料表明，上述三种人在一年内发生事故的概率依次为0.05，0.15和0.30。如果谨慎的占总的被保人数的20%，一般的占50%，冒失的占30%，(1)求某被保人在一年内发生事故的概率；(2)若此人在一年内发生事故，则他是谨慎的客户的概率是多少。 解. 设事件B 为 “被保险人在一年内出了事故” 这一事件；事件123,,A A A 分别为“谨慎的、一般的、冒失的被保险人”，则根据全概率公式可得：

112233()(|)()(|)()(|)()P B p B A p A p B A p A p B A p A =++ 3分

=0.2×0.05+0.5×0.15+0.3×0.3=0.175 5分

111112233(|)()(|)(|)()(|)()(|)()

p B A p A P A B p B A p A p B A p A p B A p A =++ 8分 =

0.050.20.05710.175

?= 10分 三、(10分)已知连续型随机变量X 有分布函数：

()arctan ,F x A B x x =+-∞<<∞，试求

(1)系数,A B ；，(2) 求概率密度()f x ；(3) X 在区间(,)a b 内取值的概率。

解.(1) ()0()1F F -∞=??∞=? 0212A B A B ππ?-=????+=?? 121A B π?=????=??

3分 (2) 2()1()()(1)dF x f x x dx x π==-∞<<∞+ 6分

(3) ()()()p a x b F b F a <<=- 8分 1111arctan (arctan )22b a ππ=

+-+ arctan arctan b a π-=

10分

.

. 昆明理工大学试卷（历年试题）

考试科目： 概率统计B(48学时) 考试日期： 命题教师：

2013年概率统计试题

一、填空题（每小题4分，共40分）

1.设A,B,C 为三个事件，则A,B,C 中至少有两个发生可表示为 。

2.已知1()4p A =，1(|)2p A B =，1(|)3

p B A =，则()p A B ?= 。 3.设事件A,B 互不相容，且1()2p A =，1()3

p B =，则()p AB = 。 4．进行独立重复实验，设每次成功的概率为p ,失败的概率为1p -,将实验进行到出

现一次成功为止，以X 表示实验次数，则()p X k == 。

5．已知随机变量X 服从参数2λ=的泊松分布，即(2)X P :，则(0)p X == 。

6．已知随机变量(2,1)X N -:，(2,1)Y N :且,X Y 相互独立，则2X Y -服从的分布

是 。

7．若随机变量X 满足()1,()2,E X D X =-=则2(31)E X -= 。

8．设12,X X 是来自于总体X 的样本，1121233X X μ=+)，2121122

X X μ=+)为总体均值μ的无偏估计，则12,μμ))中较有效的是 。

9．设12,,n X X X L 为来自总体2(,)N μσ的一个样本，2σ已知，则

212()

n i i X

X σ=-∑服从的分布是 ，2

12()n i i X μσ=-∑服从的分布是 。

10．设12,,n X X X L 为来自总体2(,)N μσ的一个样本，2σ未知，则μ的1α-的置信区

间是为 。

一、 填空题（每小题4分，共40分）

1．AB BC AC U U 2. 13 3.12

4. ()p X k ==1(1)k p p -- 1,2,k =L

5. 2e -

6.(6,5)N -

7. 8

8. 2μ)

9. 22(1),

()n n χχ-

.

. 四、(10分)已知连续型随机变量X 的概率密度函数为：220()0

0x

xe x F x x -?≥?=?<?? 求2Y X =的概率密度。

解. 显然当0,()0Y y f y ≤= 当0,y > ()()Y F y P Y y =≤ 3分 =2()P X y ≤

=(P X ≤

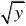
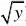
=(0P X ≤≤

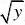
=2

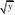
0x xe dx - 7分 '()()Y Y f y F y =

=0y y e y --=> 10分

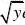
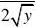
所以： 0()0

y

Y e y f y y -?>=?≤? 五、(10分)设二维随机变量(X,Y)的联合分布律如下，求

(1)a ，(2) 二维随机变量(X,Y)的 边缘分布律

(3) X,Y 是否独立 (4) E(X)，D(X)。

Y X 1 2

0 1 0.15 0.15

a 0.35

解. (1)有概率的规范性可知，0.150.150.351a +++=

所以有：0.35a = 2分

(2)

5分

(3) 因为 X Y 满足：

(,)()()i j i j p X x Y y p X x p Y y =====，1,2

0,1i j == X 1 2 p 0.5 0.5 Y 0 1 p 0.3 0.7

.

. 所以X,Y 独立。 7分

(4) ()10.520.5 1.5E X =?+?=

222()10.520.5 2.5E X =?+?=

222()()() 2.5 1.50.25D X E X E X =-=-= 10分

六、（10分）一工厂生产某种元件的寿命X （以小时计）服从参 数为160,μσ=的正态分布。

(1)若要求{}1202000.80P X <<≥，允许σ最大为多少？

(2)若{}()()20, 120200?(1.280.9,20.977)P X ФФσ=<<===

解. (1)P{120<X<200}=}160200160160120{σ

σσ-<-<-X P =)40()40(

σσ-Φ-Φ=2)40(σΦ-1 80.0≥ 即 )28.1()40(Φ≥Φσ 亦 25.3128

.140=≤

σ； 5分 (2)当σ=20时，P{120<X<200}=}20

1602002016020160120{-<-<-X P =2)20

40(Φ-1=2)2(Φ-1=0.954. 10分

七、(10分)设12,,n X X X L 为来自于总体 X 的一个样本, 总体 X 的密度函数为

|

|1(),2x f x e x θθ-=-∞<<∞，求参数θ的极大似然估计?θ。

解

1()(,)n

i i L f x θθ==∏ 2分

1||||111022n i i i x n x n i e e θθθθθ=--=∑??==> ???

∏ 5分 11ln ()ln 2||n

i

i L n x θθθ==--∑ 7分

. . 21ln ()1||0n

i

i d L n x d θθθθ=-=+=∑ 9分 1

1?||n i i x n θ==∑ 10分

2012年概率统计试题（部分）

一、填空题（每小题4分共40分）

1．某市有50%的住户订阅日报，65%的住户订阅晚报，85%的住户至少订阅这两种报纸中的一种，则同时订阅这两种报纸的住户所占的百分比为 。

2．一批产品中一、二、三等品各占60%，30%，10%，从中随机抽取一件，发现不是三等品，则取到一等品的概率为 。

3．设随机变量~(2),X E c 是X 的可能取值，则()P X c == 。

4．设随机变量~(2,)X B p ，则2()E X = 。

5．设随机变量X 与Y 独立同分布，且1(1)(1)2P X P X =-===，则()D X Y -= 。

6．设随机变量X 与Y 的联合密度为

1,0,1(,)0,

x y f x y <<?=??其他 则~X 。

7．设1234,,,X X X X 是取自正态总体(0,1)N 的样本，

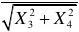
~ 。 8．F 分布的分位数12(,)F n n α与121(,)F n n α-之间的关系是 。

9．设事件A 发生的概率是?,n p p

是n 次独立重复试验中A 发生的频率，若用?n p 作为p 的估计，则?n p 是p 的 估计。

10．设12,,...,n x x x 是取自正态总体2(,)N μσ的样本值，x 与2

s 分别是样本均值与方差，

其中2,μσ均未知，若置信水平为1α-，则μ的置信区间为 。

二、（12分）设随机变量X 的分布函数为

. . 0,1()arcsin ,2

1,

x a x F x A a x a a x a ≤-???=+-<≤??>??， 试求 （1）常数A ；（2）()2a P X <

；（3）密度函数()f x 。

三、（10分）在电源电压不超过200V 、200-240V 、超过240V 三种情况下，某电子元件损坏的概率分别为0.1、0.001、0.2，假设电压2~(220,25)X N ，试求电子元件损坏的概率（(0.8)0.7881Φ=）。

四、（12分）假设10只同种元件中有2只次品，从中任取一只，若是次品，则扔掉重取一只；若仍是次品，则扔掉再取一只。试求在取到正品前，取出的次品数X 的分布律及方差()D X 。

六、（8分）设随机变量X 与Y 的联合密度为

221,1(,)0,

x y f x y π?+<?=???其他

试判定X 与Y 是否独立。

五、（8分）设有下表

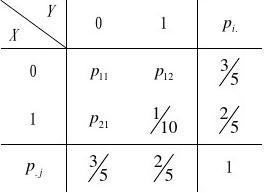
试求X 与Y 的联合分布律及[min(,)]E X Y 。

.

. 2010年概率统计试题（部分）

一、填空题（每小题4分，共40分）

1、设A 、B 、C 构成一完备事件组，且()0.5P A =，()0.7P B =，则()P C = 。

2、设某种动物从出生算起活20年以上的概率为0.8，活25年以上的概率为0.4。现年20岁的这种动物能活25岁以上的概率是 。

3、某人向目标射击，直到击中目标为止，设各次击中与否相互独立且每次击中目标的概率为()01p p <<，则射击次数X 的分布律是 。

4、设每对夫妇的子女数

X 服从参数为λ的泊松分布,且知一对夫妇有不超过1个孩子的概率为23e -，则任选一对夫妇至少有3个孩子的概率是 。

5、设[]1,6X U :，则二次方程210x Xx ++=有实根的概率是 。

6、设(),E X μ=2

()D X σ=,则对任意正数ε，有()P X με-<> 。

7、设X 与Y 的联合概率密度： ()2,01,0,x y f x y <<<?=??其他

，则P(X+Y 1)=≤ 。 8、设X 与Y 独立同分布于()0,1N ,则X 与Y 的联合概率密度(),f x y = 。

9、设总体()20,X N σ:,12,......n X X X 是X 的样本，则122

2......n X X σ++: 。 10、设(),E X μ=2()D X σ=，123,,X X X 是X 的样本，()1121?2

X X μ=+，()21231?3

X X X μ=++.12??,μμ作为μ的估计量，较有效的是 。

二、（10分）报台分别以概率0.6，0.4发出信号“.”与“—”，由于通讯系统受到干扰，当发出信号“.”，收报台未必收到信号“.”，而是分别以概率0.8与0.2收到信号“.”与“—”，当发出信号“—”，收报台分别以概率为0.9与0.1收到信号“—”与“.”时，求

（1）收报台收到信号“—”的概率；

（2）当收报台收到信号“—”时，发报台确实发出信号“—”的概率。

三、（15分）设连续型随机变量X 的概率密度为

. . 3,0()0,

x ae x f x -??>=???其它， 求：（1）未知系数a ；（2）X 的分布函数()F x ；（3）{3}X <的概率。

四、（10分）设~(1,1)X N ，2(1)Y X =-，试求Y 的概率密度()Y f y 。

五、（10分）设X 服从参数为1λ=的指数分布，随机变量

1,,1,20,k X k X k X k >?==?≤?

（1）求1X 与2X 的联合分布律；

（2）判定1X 与2X 是否独立。

六、（10分）设0.5,1.25,0.80,2.00是来自总体X 的样本值，已知()Y=lnX N ,1μ:,

试求：

（1）μ的矩估计；

（2）μ的置信水平为95%的置信区间. ()0.0250.025 1.96u z ==。

七、（5分）设流水线上生产的某零件内径()11,1X N :，已知销售利润T 与内径X 有如下关系：

20,10125,X T ≤≤?=?-?

其他 求销售一个零件的平均利润()E T 。()()10.8413Φ=

.

. 《概率论与数理统计》（2005年）期末试卷（部分试题）

一．填空题（每小题3分）

1．设A 、B 是相互独立的随机事件，P (A )=0.5, P (B )=0.7, 则()P A B U =_____.

2．设随机变量~(,), ()3, () 1.2B n p E D ξξξ==，则n =______.

3．随机变量ξ的期望为()5E ξ=，标准差为()2σξ=，则2

()E ξ=_______.

4．甲、乙两射手射击一个目标，他们射中目标的概率分别是0.7和0.8.先由甲射击，若甲未射中再由乙射击。设两人的射击是相互独立的，则目标被射中的概率为_________. 1．0.85、2. n =5、3. 2()E ξ=29、4. 0.94

二． (本题10分) 设随机变量ξ的分布密度为 , 03()10, x<0x>3

A x f x x ??=+???当≤≤当或

(1) 求常数A ; (2) 求P (ξ<1)； (3) 求ξ的数学期望.

解：（1）

??

∞∞-==+=3

4ln 1,4ln 1)(A A dx x A dx x f ---------------------3分 （2）?==+=

<10

212ln 1)1(A dx x A P ξ-------------------------------6分 （3）3

300()()[ln(1)]1Ax E xf x dx dx A x x x ξ∞-∞=

==-++?? 13(3ln 4)1ln 4ln 4

=-=-------------------------------------10分

三． (本题10分)有10盒种子，其中1盒发芽率为90％，其他9盒为20％.随机选取其中1盒，从中取出1粒种子，该种子能发芽的概率为多少？若该种子能发芽，则它来自发芽率高的1盒的概率是多少？

解：由全概率公式及Bayes 公式

P (该种子能发芽)＝0.1×0.9+0.9×0.2＝0.27-----------------------------------5分 P (该种子来自发芽率高的一盒)＝(0.1×0.9)/0.27＝1/3---------------------10分

四．(本题12分) 某射手参加一种游戏，他有4次机会射击一个目标.每射击一次须付费10元. 若他射中目标，则得奖金100元，且游戏停止. 若4次都未射中目标，则游戏停止且他要付罚款100元. 若他每次击中目标的概率为0.3,求他在此游戏中的收益的期望.

.

. 解. 令A k ={在第k 次射击时击中目标}，A 0={4次都未击中目标}。

于是P (A 1)=0.3; P (A 2)=0.7×0.3=0.21; P (A 3)=0.72

×0.3=0.147

P (A 4)= 0.73×0.3=0.1029; P (A 0)=0.74=0.2401-----------------------------------6分

在这5种情行下，他的收益ξ分别为90元，80元，70元，60元，－140元。-------------------------------------------------------------------------------------------8分

因此， 65

.26)140(2401.0601029.070147.08021.0903.0)(=-?+

?+?+?+?=ξE

--------------------12分 五．测量某冶炼炉内的温度，重复测量4次，数据如下（单位：℃）：

1820，1834，1830，1816

假定重复测量所得温度2

~(,)N ξμσ. 10σ=，求总体温度真值μ的0.95的置信区间. (注：(1.96)0.975Φ=,(1.65)0.95Φ=) 解：1(1820183418301816)18254

ξ=

+++=-------------------2分 已知10.95, 0.05αα-==，0.0252

1.96u u α==---------------------------5分 10σ=，

n=4, 0.02529.8u u α

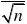
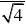
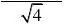
===-------------------8分 所求真值μ的0.95的置信区间为[1815.2, 1834.8]（单位：℃）-------10分