A ′ G D

B

C A 第6题 2015年醴陵一中创新实验班招生考试

数学试题

考生注意：本卷满分100分，考试时间120分钟，请将答案写在答题卡上。

一、选择题（本题共10个小题，每小题3分，满分30分）

1．把抛物线22y x =-+1向下平移1个单位，再向左平移1个单位，得到的抛物线是（ ）。

A ．22(1)y x =-+

B ．22(1)y x =--

C ．221y x =-+

D ．2

21y x =-- 2．甲、乙两学生在军训打靶训练中，打靶的总次数相同，且所中环数的平均数也相同， A ．＜ B ．＞ C ．= D ．不能确定

3．已知两圆的半径分别为6和1，当它们外切时，圆心距为（ ）。

A ．5

B ．6

C ．7

D ．8

4．如图，用两根等长的钢条AC 和BD 交叉构成一个卡钳，可以用来

测量工作内槽的宽度.设OA OB m OC OD

==，且量得CD b =，则内槽 的宽AB 等于（ ）。 B.m b C.b m D.1

b m + 5．小明在二次函数y=2x 2+4x+5的图象上，依横坐标找到三点（－3，y 1），（－1，y 2）， （2，y 3），则你认为y 1，y 2，y 3的大小关系应为（ ）

A ．y 1＞y 2＞y 3

B ．y 2＞y 3＞y 1

C ．y 3＞y 1＞y 2

D ．y 3＞y 2＞y 1

6．如图，矩形纸片ABCD 中，AB=4，AD=3，折叠纸片使AD 边与对角

线BD 重合，折痕为DG ，则AG 的长为（ ）

A ．1

B ．34

C ．23

D ．2 7．如图，小正方形的边长均为1，则图中三角形（阴影部分）与△ABC 相似的是( )。

A B D C b A B

第4题 O

8．若抛物线c bx ax y ++=2的顶点在第一象限，与x 轴的两个交点分布在原点两侧，则点（—a ，—a c ）在（ ）。 A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 9．如图，直线1y x 2=

与双曲线k y x =（k ＞0，x ＞0）交于点A ，将直线1y x 2

=向上平移4个单位长度后，与y 轴交于点C ，与双曲线k

y x

=（k ＞0，x ＞0）交于点B ，若OA=3BC ，则k 的值为（ ） A 、3 B 、6 C 、

94 D 、92

10．如图，AB 是⊙O 的直径，且AB=10，弦MN 的长为8，若弦

MN 的两端在圆上滑动时，始终与AB 相交，记点A 、B

到MN 的距离分别为h 1，h 2，则|h 1－h 2| 等于（ ）

A 、5

B 、6

C 、7

D 、8

二、填空题（本题共6个小题，每小题3分，满分18分）

11、观察图象，直接写出一元二次不等式： 的解集是____________。

12． 如图，C 为线段AB 上的一点，△ACM 、△CBN 都是等边三角形，若AC ＝3，BC ＝2，则

△MCD 与△BND 的面积比为_________。

13． 在半径为1cm 的圆中，圆心角为270°的扇形的弧长是________cm 。

14．抛物线22(1)1(02)y x x =+-≤<的最小值是___ 。 第11题 A B C D M

N 第12题

人数 15．如图，平面直角坐标系中，已知直线y x =上一点

P （1，1），C 为y 轴上一点，连接PC ，线段PC 绕

点P 顺时针旋转900至线段PD ，过点D 作直线

AB ⊥x 轴。垂足为B ，直线AB 与直线y x =交于

点A ，且BD=2AD ，连接CD ，直线CD 与直线y x

=交于点Q ，则点Q 的坐标为 。

16．定义符号min{a ，b}的含义为：当a≥b 时min{a ，b}=b ；当a ＜b 时min{a ，b}=a ．如：

min{1，﹣3}=﹣3，min{﹣4，﹣2}=﹣4．则min{﹣x 2+1，﹣x}

的最大值是 。

三、解答题（本题共2个小题，每小题4分，满分8分）

17、计算2)

21(3160tan 12--+--︒-

18、求不等式组⎪⎩

⎪⎨⎧<+--≤-12312)2(25x x x x 的整数解. 四、解答题（本题共2个小题，每小题6分，满分12分）

19、今年以来，我国持续大面积的雾霾天气让环保和健康问题成为焦点．为了调查学生对

雾霾天气知识的了解程度，某校在学生中做了一次抽样调查，调查结果共分为四个等级：A ．非常了解；B ．比较了解；C ．基本了解；D ．不了解．根据调查统计结果，绘制了不完整的两种统计图表．

请结合统计图表，回答下列问题．

（1）本次参与调查的学生共有 人.

（2）扇形统计图中B 部分扇形所对应的圆心角是 度.

（3）请补全条形统计图.

（4）根据调查结果，学校准备开展关于雾霾知识竞赛，某班要从A 等级中的小明和小刚

中选一人参加，现设计了如下游戏来确定，具体规则是：把四个完全相同的乒乓球标上数字1，2，3，4，然后放到一个不透明的袋中，一个人先从袋中随机摸出一个球，另一人再从剩下的三个球中随机摸出一个球．若摸出的两个球上的数字和为奇数，则小明去；否则小刚去．请用树状图或列表法求出他们各自去的概率，并说明规则是否公平。

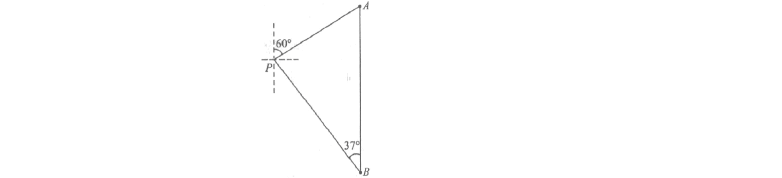
20、周末，小亮一家在梅溪湖游玩，妈妈在湖心岛P 处观看小亮与爸爸在湖中划船（如图），

小船从P 处出发，沿北偏东60°方向划行200米到A 处，接着向正南方向划行一段时间到B 处.在B 处小亮观测妈妈所在的P 处在北偏西37°的方向上，这时小亮与妈妈相距多少米（精确到1米）？

（参考数据：73.13,41.12,75.037tan ,8.037cos ,6.037sin ≈≈≈︒≈︒≈︒）

五、解答题（本题共3个小题，21、22每题10分，23题12分，共32分）

21、经统计分析，我市咸嘉湖隧道的车流速度v （千米／小时）是车流密度x （辆／千米）

的函数，当隧道中的车流密度达到220（辆／千米）时，造成堵塞，此时车流速度为O 千米/小时；当车流密度不超过20（辆／千米）时，车流速度为80（千米／小时）。研究表明：当20≤x≤220时，车流速度v 是车流密度x 的一次函数．

（1）求隧道中车流密度为100（辆／千米）时的车流速度；

（2）在交通高峰时段，为使隧道中的车流速度大于40（千米／小时）且小于60（千

米／小时）时，应控制隧道中的车流密度在什么范围内？

（3）车流量（辆／小时）是单位时间内通过隧道中某观测点的车辆数，即：车流量=

车流速度×车流密度．求隧道中车流量y 的最大值．

22、如图，AB、AC分别是⊙O的直径和弦，点D为劣弧AC上一点，弦DE⊥AB分别交⊙O

于E，交AB于H，交AC于F．P是ED延长线上一点且PC=PF．

（1）求证：PC是⊙O的切线；

（2）点D在劣弧AC什么位置时，才能使2

=⋅，为什么?

AD DE DF

（3）在（2）的条件下，若OH=1，AH=2，求弦AC的长．

23、如图，点A与点B的坐标分别是（1，0），（5，0），点P是该直角坐标系内的一个动

点．

（1）使∠APB=30°的点P 有个；

（2）若点P在y轴上，且∠APB=30°，求满足条件的点P的坐标；

（3）当点P在y轴上移动时，∠APB是否有最大值？若有，求点P的坐标，并说明此时∠APB最大的理由；若没有，也请说明理由．

A B