高等数学（上）

第一章 函数与极限

1. 设 ?????≥<=3||,03|||,sin |)(ππ?x x x x , 求).2(446?π?π?π?、、、??

? ??-??? ????? ?? 2. 设()x f 的定义域为[]1,0，问：⑴()2x f ； ⑵()x f sin ；

⑶()()0>+a a x f ； ⑷()()a x f a x f -++ ()0>a 的定义域是什么？

（1）][；，－的定义域为所以知－11)(,11102

2x f x x ≤≤≤≤ 3. 设()?????>-=<=1110

11x x x x f ，()x

e x g =，求()[]x g

f 和()[]x f

g ，并做出这两个函数的图形。

4. 设数列{}n x 有界, 又,0lim =∞→n n y 证明: .0lim =∞→n n n y x

5. 根据函数的定义证明:

⑴ ()813lim 3

=-→x x (2) 0sin

lim =+∞

→x x x 6. 根据定义证明: 当0→x 时,函数x x y 21+

=是无穷大.

问x 应满足什么条件时,才能使?104>y

7. 求极限:

⑴ 13lim 223+-→x x x =0

⑵ ()h

x h x h 220lim -+→=x h h x

h h 2)2(lim 0=+→ ⑶ 13lim 242+-+∞→x x x x x =0

(4) ()2121lim n n n -+++∞→Λ=212)1(lim 2=-∞→n n n n (5) ??? ??---→311311lim x x x =1)

1)(1(31lim 221-=++--++→x x x x x x (6) ()22

3222lim -+→x x x x =∞ 8. 计算下列极限: ⑴ x x x 1sin lim 20

→=0 ⑵ x x x arctan lim ∞→=0arctan .1lim =∞→x x

x 9. 计算下列极限:

⑴ x x x ωsin

lim 0→=????=→.sin lim 0

x x x ⑵ x x x 3tan

lim 0→=33cos 1.3sin

lim 0

=→x x x x ⑶

x x x x sin 2cos 1lim 0-→=2sin .sin 2lim 20=→x x x x (4)x x x 321??? ??-∞→lim = 6620)21(lim ---→=??????-e x x x

（5）()x

x x 1

021+→lim =22.210)21(lim e x x x =+→

高等数学（上）

第一章 函数与极限

1. 设 ?????≥<=3||,03|||,sin |)(ππ?x x x x , 求).2(446?π?π?π?、、、??

? ??-??? ????? ?? 2. 设()x f 的定义域为[]1,0，问：⑴()2x f ； ⑵()x f sin ；

⑶()()0>+a a x f ； ⑷()()a x f a x f -++ ()0>a 的定义域是什么？

（1）][；，－的定义域为所以知－11)(,11102

2x f x x ≤≤≤≤ 3. 设()?????>-=<=1110

11x x x x f ，()x

e x g =，求()[]x g

f 和()[]x f

g ，并做出这两个函数的图形。

4. 设数列{}n x 有界, 又,0lim =∞→n n y 证明: .0lim =∞→n n n y x

5. 根据函数的定义证明:

⑴ ()813lim 3

=-→x x (2) 0sin

lim =+∞

→x x x 6. 根据定义证明: 当0→x 时,函数x x y 21+

=是无穷大.

问x 应满足什么条件时,才能使?104>y

7. 求极限:

（6）x x x x ??? ??--∞→13lim =21)2.(21)121(lim -+--∞→=-+e x x x

10. 利用极限存在准则证明:

⑴ 11211lim 222=??? ??++++++∞→πππn n n n n n Λ

故原式＝1

⑵ 数列ΛΛ,222,22,2+

++的极限存在,并求其极限.

11. 当0→x 时, 22x x -与32x x

-相比, 哪一个是较高阶

的无穷小? 12. 当1→x 时, 无穷小x -1和()212

1x -是否同阶?是否等价?

13. 证明: 当0→x 时, 有2~1sec 2

x x -.

14. 利用等价无穷小的代换定理, 求极限: x x

x x 30sin sin tan lim -→.

15. 讨论()201212x x f x x x ?≤<=?-≤≤? 的连续性, 并画出其图

形.

16. 指出下列函数的间断点属于哪一类.若是可去

间断点,则补充或改变函数的定义使其连续. ⑴ 2,123122==+--=x x x x x y

⑵ 11311=???>-≤-=x x x x x y

1x y ==0

17. 讨论函数()x x x x f n n

n 2211lim +-=∞→的连续性, 若有间断点,

判别其类型。

18. 求函数 ()633223-+--+=x x x x x x f 的连续区间, 并求()()x f x f x x 30lim ,lim -→→.

19. 求下列极限：

⑴ 52lim 20+-→x x x =5

⑵ ()3

2sin lim 4

απ

α→=1 ⑶ ααα--→x x x sin sin lim αα

αααcos 2cos 2sin 2lim =-+-=→x x x x ⑷ ()x x x x x --++∞→22lim 12lim

22=-++=+∞→x x x x x

x ⑸ x x e 1lim ∞→101

lim ===∞→e e x x

⑹ x x x sin ln lim 0→01ln sin lim ln 0

==??????=→x x x ⑺ 211lim x x x ??? ??+∞→2

1211)11(lim e x x x =??????+=∞→

20. 设函数

()???≥+<=00x x a x e x f x , 应怎样选择a ，使()x f 在()+∞∞-,内连续。

21. 证明方程b x a x +=sin 其中,0,0>>b a 至少有一正根，并且它不超过b a +.

22. 若()x f 在[]b a ,上连续，b x x x a n <<<<<ΛΛ21, 则在[]n

x x ,1上必有ξ, 使()()()()n x f x

f x f f n Λ++=21ξ.

23. 证明: 若()x f 在()+∞∞-,内连续, ()x f x ∞→lim 存在, 则()x f 必

在()+∞∞-,内有界

. []{}内有界。

在，即，有则对，

＝取使即上连续，故有界在又即成立时，有当，，对证明：设),()()(),(1,max )(,,)(1)(,1)(1)(lim 111+∞-∞≤+∞-∞∈?+≤?-+<<->?==∞→x f M x f x A M M M x f M X X x f A

x f A x f X x X A x f x ε 第二章???导数与微分 典型例题解析

例1 设()f x 在0x 处可导，求000()(3)lim x f x x f x x x

→+--． 分析 所求极限与0()f x '的定义式子很相似，则由0()f x '的定义即可求解．

解 000()(3)lim x f x x f x x x →+--=00000[()()][()(3)]lim x f x x f x f x f x x x

→+-+-- =000000()()(3)()lim 3lim 3x x f x x f x f x x f x x x

→→+---+- =00()3()f x f x ''+=04()f x '．

错误解答 令03x x t -=，则03x x t =+，

000()(3)lim x f x x f x x x →+--=0(4)()lim x f t x f t x

→+-=04lim ()x f t →' （1）

=00

4lim (3)x f x x →'-=04()f x '． （2） 错解分析 式（1）用到()f x 在点t 的导数；式（2）用到()f x '在点0x 连续．但是题目只是给出()f x 在0x 处可导的条件，而()f x 在0x 的邻域内是否可

导以及()f x '在0x 处是否连续都未知．所以上述做法中的式（1）与式（2）

有可能不成立．

例2 设()()()f x a bx a bx ??=+--，其中()x ?在(,)-∞+∞上有定义且在点a 处可导．试求(0)f '．

分析 求函数在某一点的导数可以用导数的定义来求；也可先求导函数，然后求导函数在该点的函数值，但在本题中函数()f x 的可导性未知，故只能用定义来求．

解 当0b ≠时，0()(0)lim 0x f x f x →--=0()()lim x a bx a bx x

??→+-- =0[()()][()()]lim x a bx a a bx a x

????→+---- =00()()()()lim lim x x a bx a a bx a b b bx bx

????→→+---+- =()()b a b a ??''+=2()b a ?'．

所以(0)f '=2()b a ?'．

当0b =时，()0f x =，(0)0f '=．

综上所述，(0)f '=2()b a ?'．

例3 设函数2()()()f x x a x ?=- ，其中()x ?的一阶导函数有界．求()f a ''． 分析 求函数在某一点的二阶导数可以用导数的定义来求，但必须先求出一阶导数；也可先求出二阶导函数，然后求二阶导函数在该点的函数值，但在本题中函数()f x '的可导性未知，故只能用定义来求．

解 由于2()2()()()()f x x a x x a x ??''=-+-，则有()0f a '=．又

()()lim x a f x f a x a

→''--=22()()()()lim x a x a x x a x x a ??→'-+-- =lim[2()()()]x a

x x a x ??→'+-=2()a ?, 所以()f a ''=2()a ?．

错误解答 因为

2()2()()()()f x x a x x a x ??''=-+-，

2()2()2()()2()()()()f x x x a x x a x x a x ????''''''=+-+-+-，

所以()f a ''=2()a ?．

错解分析 此解法错误的根源在于()x ?的一阶导函数有界并不能保证

()x ?二阶可导．而上述求解却要用到()x ?''．

注 此题用到如下结论：

a ．有界量与无穷小的乘积仍为无穷小；

b ．可导必连续．

例4 设()f x 的一阶导数在x a =处连续且0()lim 1x f x a x

→'+=，则（ ）． A ．()f x 在x a =处的二阶导数不存在． B ．0

lim ()x f x a →''+一定存在． C ．()1f a ''=． D ．()2f a '=．

解 因为0()lim 1x f x a x

→'+=，所以0lim ()0x f x a →'+=，由于()f x '在x a =处连续，故 ()0f a '=． 又因为00()()()lim lim 1()x x f x a f a f x a x a a x

→→'''+-+==+-，所以()1f a ''=．选C ． 例5 设()f x 在0x =的某个邻域内有定义，x 、y 为该邻域内任意两点且()f x 满足条件：

（1）()()()1f x y f x f y +=++；

（2）(0)1f '=．

试证在上述邻域内()1f x '=．

分析 此处无法用求导公式和求导法则证明()1f x '=．由于()f x 的表达式未给出，故只能考虑从定义出发．如果用条件（2），则需先求出(0)f ．

证明 因为()f x 在0x =的某个邻域内有定义，记该邻域为E ，则对任意x 、y E ∈，有()()()1f x y f x f y +=++．令0y =，则(0)1f =-．于是对任意x E ∈，当x x E +?∈及x E ?∈时，考虑下列极限

0()()lim x f x x f x x ?→+?-?=0[()()1]()lim x f x f x f x x

?→+?+-? =0()(1)lim x f x x

?→?--? =0()(0)lim x f x f x

?→?-? =(0)f '=1，

故()1f x '=，x E ∈．

例6（04研） 设函数()f x 连续，且(0)0f '>，则存在0δ>，使得（ ）．

A ．()f x 在(0,)δ内单调增加．

B ．()f x 在(,0)δ-内单调减少．

C ．对任意的(0,)x δ∈有()(0)f x f >．

D ．对任意的(,0)x δ∈-有()(0)f x f >． 解 由导数定义知

0()(0)(0)lim 00

x f x f f x →-'=>-． 根据极限的保号性，知存在0δ>，当(,0)(0,)x δδ∈-U 时，有

()(0)0f x f x

->． 因此

当(,0)x δ∈-时，有()(0)f x f <；当(0,)x δ∈时，有()(0)f x f >，故选C ． 注 函数()f x 只在一点的导数大于零，一般不能推导出单调性，题设告诉函数在一点可导时，一般应联想到用导数的定义进行讨论．

例7 设不恒为零的奇函数()f x 在0x =处可导．试说明0x =为函数()

f x x

的哪一类间断点．

解 由题设知()()f x f x -=-，令0x =可得(0)0f =．则

0()lim x f x x →=0()0lim 0

x f x x →--=(0)f '， 于是()

f x x 在0x =处有极限．从而0x =是()

f x x 的可去间断点．

例8 设函数()f x 可导，()()(1sin )F x f x x =+，则(0)0f =是()F x 在0x =处可导的（ ）．

A ．充分必要条件 ．

B ．充分条件但非必要条件．

C ．必要条件但非充分条件．

D ．既非充分条件又非必要条件． 分析 ()F x 表达式中含有绝对值符号，又要考查函数在一点的导数的存在性，因此要考虑函数的左右导数．

解 由导数定义

0()(0)(0)lim 0

x F x F F x →-'=-， 知

(0)(0)(0)(0)f f f f -''=-=-，

(0)(0)(0)(0)f f f f +''=+=+，

可见(0)F '存在(0)(0)F F -+''?=，即(0)0.f =故选A ．

例9（01研） 设(0)0f =，则()f x 在点0x =可导的充要条件为（ ）．

A ．201lim (1cosh)h f h

→-存在． B ．01lim (1)h h f e h →-存在． C ．201lim (sinh)h f h h →-存在． D ．01lim [(2)()]h f h f h h

→-存在． 分析 本题主要考查导数的定义，另外也考查了某些无穷小量的阶以及它们的正负号．

解 注意到1cosh 0-≥，且0

lim(1cosh)0h →-=． 如果201lim (1cosh)h f h →-存在．则

001(1cosh)(0)1()(0)1lim lim (0)21cosh 0202

h u f f f u f f u ++→→---'===---． 所以A 成立只保证(0)f +'存在，而不是(0)f '存在的充分条件． 如果01lim (1)h h f e h

→-存在，则 0()(0)(1)lim (0)0

u f u f f u →-'=-=--， 故B 是(0)f '存在的充要条件．

对于C ，

22

1(sinh)(0)sinh (sinh)sinh 0f h f h f h h h h ----=?--， 注意到20sinh lim 0h h h →-=，所以若(0)f '存在，则由右边推知左边极限存在且为零．若左边极限存在，则由

知上式左边极限可能不存在，故(0)f '可能不存在．

至于D ，

00111lim [(2)()]lim ((2)(0))(()(0))h h f h f h f h f f h f h h h →→??-=---????

， 若(0)f '存在，上述右边拆项分别求极限均存在，保证了左边存在．而左边存在，不能保证右边拆项后极限也分别存在．故选B ．

例10（99研）

设

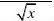
20()(),0x f x x g x x >=?≤? ，其中()g x 是有界函数，则()f x 在0x =处（ ）．

A ．极限不存在．

B ．可导．

C ．连续但不可导．

D ．极限存在但不连续．

解 由于

0()(0)lim 0

x f x f x -→--=20()lim x x g x x -→?=0=(0)f -'， 0()(0)lim 0x f x f x +→--

=0lim x +→=0=(0)f +'，

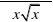
故选B ．

例11 已知()f x 在x a =处可导且()0f a >．求1()lim[]()n n f a n f a →∞+． 分析 题目条件是()f x 在x a =处可导，必然有()f x 在x a =处连续，从而可知该极限属于1∞型．

解 ()f x 在x a =处可导．则 且当n 充分大时1()0f a n

+>．故 1()lim[]()n n f a n f a →∞+=1()exp{lim ln }()

n f a n n f a →∞+? =1()()exp{lim ln[1]}()

n f a f a n n f a →∞+-?+ =1()()exp{lim }()

n f a f a n n f a →∞+-? =1()()1exp{lim }1()

n f a f a n f a n

→∞+-?=()exp{}()f a f a '． 注 此题用到当0x →时，ln(1)x x +:． 例12 讨论函数()|(1)|f x x x x =-的可导性． 分析 ()f x 的表达式含有绝对值符号，应先去掉绝对值符号，本质上()f x 为分段函数．

解法1 由(1)0x x -≥可得1x ≥或0x ≤．由(1)0x x -<得01x <<．于是

3223,10(),01x x x x f x x x x ?-≥≤?=?-<<??

或， 可求得

2232,10()23,01x x x x f x x x x ?-><?'=?-<<??

或， 因为 0()(0)lim 0

x f x f x +→--=230lim x x x x +→-=0， 0()(0)lim 0x f x f x -→--=320lim 0x x x x -→-=，

所以(0)0f '=，即()f x 在0x =处可导．而

1()(1)lim 1

x f x f x +→--=321lim 1x x x x +→--=1， 1()(1)lim 1x f x f x -→--=231lim 1x x x x -→--=1-，

则()f x 在1x =处不可导．

综上所述()f x 在1x =处不可导，()f x 在(,1)(1,)-∞+∞U 上均可导． 解法2

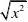
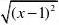
依题意，()f x x =且仅在0x =和1x =处可能不可导．故只需讨论在这两点的情形．

（1）0x =时，由于

0|||1|lim 00

x x x x x →??-=-， 故(0)0f '=．

（2）1x =时，由于

1|||1|lim 1

x x x x x →??--不存在， 故()f x 只在1x =处不可导，在(,1)(1,)-∞+∞U 上均可导．

解法3 由于

()|(1)||||1|f x x x x x x x =-=?-，

由导数定义可知，||x 在0x =处不可导，而||x x 在0x =处一阶可导，因此，||x x 在任意点处均可导，再只需考查|1|x -的可导性．由导数定义可知，|1|x -仅仅在1x =处不可导，故()f x 仅在1x =处不可导，在(,1)(1,)-∞+∞U 上均可导．

例13 设2()lim 2tx t x f x x e

→+∞=+-，讨论()f x 的可导性． 分析 先应求出()f x 的表达式．本质上()f x 为分段函数． 解 由于

,0lim 1,00,0tx t x e x x →+∞+∞>??==??<?

， 则有

2

0,0(),02x f x x x x ≥??=?<?+? ． 显然当0x >或0x <时，函数()f x 可导．下面讨论0x =时()f x 的可导性．由于

(0)f +'=0()(0)lim 0x f x f x +→--=000lim x x +→-=0，

(0)f -'=0()(0)lim 0x f x f x -→--=2002lim x x x x -→-+=12

， 于是(0)f +'≠(0)f -'，从而可知()f x 仅在0x =处不可导．

例14（05研）

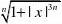
设函数()n f x =()f x 在(,)-∞+∞内（ ）． A ．处处可导． B ．恰有一个不可导点．

C ．恰有两个不可导点．

D ．至少有三个不可导点． 解 由于

()n f x =133lim[||(1||)]n n n n x x -→∞+=133lim ||(1||)n n n x x -→∞+

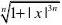
易求得

33,1()1,11,

1x x f x x x x ?>?=-≤≤??-<-?，

则

310()(1)1(1)lim lim 311

x x f x f x f x x +++→→--'===--， 11()(1)11(1)lim lim 01

1x x f x f f x x ---→→--'===--， 故1x =为不可导点．同理1x =-也为不可导点．故选C ．

例15 设12()max{(),()}F x f x f x =的定义域为(1,1)-，其中

1()1f x x =+，22()(1)f x x =+，

试讨论()F x 的可导性．若可导，求其导数．

分析 本质上()F x 是分段函数即

112212

(),()()()(),()()f x f x f x F x f x f x f x ≥?=?<?， 由此可知需先解出不等式

12()()11f x f x x ≥??-<<? 与 12()()

11f x f x x <??-<<?．

解 由12()()11f x f x x ≥??-<<?即21(1)11x x x ?+≥+?-<<?解得10x -<≤，此时()1F x x =+．

而由12()()11f x f x x <??-<<?即21(1)11x x x ?+<+?-<<?解得01x <<，此时2()(1)F x x =+．则有

且

当0x =时，

0()(0)lim 0

x F x F x +→--=20(1)1lim x x x +→+-=2， 0()(0)lim 0x F x F x -→--=0(1)1lim x x x

-→+-=1， 即(0)(0)F F +-

''≠，所以()F x 在0x =处不可导．故 1,10()2(1),01x F x x x -<<?'=?+<<?

　　　　． 例16 设函数21()1

x

e x

f x ax b x ?≤?=?+>??，若要()f x 为可导函数，应如何选择,a b ？ 解 显然当1x >及1x <时，()f x 可导，故要使()f x 为可导函数，只需使其在1x =处可导．由可导与连续的关系，应该首先选择,a b ，使其在1x =连续．因

(1)f e =，(1)f e -=，(1)f a b +=+，

故当a b e +=即b e a =-时，()f x 在1x =连续．又

22

121111()(1)11(1)lim lim lim lim 2111

1x x x x x x f x f e e e x f e e e x x x x ------→→→→----'=====----， 111()(1)()(1)lim lim lim 111x x x f x f ax b e ax e a e f a x x x ++++→→→-+-+--'====---， 因此当2,a e b e ==-时，(1)f '存在，从而()f x 为可导函数．

例17 设()sin f x x =，2()x x ?=．求[()]f x ?'，[()]f x ?'，[(())]f x ?'． 分析 三个函数中都有导数记号，其中[()]f x ?'表示函数()x ?对x 求导，求得()x ?'后再与f 复合；[()]f x ?'表示函数f 对()x ?求导，即()f u 对u 求导，而()u x ?=；[(())]f x ?'表示复合函数[()]f x ?关于自变量x 求导．

解 ()cos f x x '=，()2x x ?'=．则

[()]f x ?'=(2)f x =sin 2x ，[()]f x ?'=2cos x ，

以及

[(())]f x ?'=[()]()f x x ??''?=22cos x x ．

例18 设21ln sin ()x y x -=．求dy dx

． 分析 本题既可直接由复合函数求导法则求导，也可利用微分的形式不变性先求出dy ，然后可得dy dx

． 解法1 直接由复合函数求导法则，令sin u v =，1ln x v x -=，则

dy

dx =dy du dv du dv dx

?? =2ln 22cos x

u v x

-?? =2ln 21ln sin 2()x

x x x

--?． 解法2 利用一阶微分的形式不变性

dy =21ln sin ()x d x -=1ln 1ln 2sin()sin()x x d x x

-- =1ln 1ln 1ln 2sin()cos()()x x x d x x x ---=2ln 21ln sin 2()x

x dx x x --?

故

dy

dx =ln 21ln sin 2()2x x x

x --?． 例19 设a a x a x a y x

a a =++，0a >．求dy dx ． 分析 a a x 为幂函数；a x a 为指数函数与幂函数复合而成的函数；而x a a 也

为复合函数，它是指数函数与指数函数复合而成的函数．

解 dy dx =()()()a a x a x a x a a '''++=1ln ln ()()a a x a a x a a a a x e e -??''?++

=1ln ()ln ()a a x a a x a a x a

x a a x a a a -''?+??+?? =112ln (ln )a a x a a x a a x a

x a a a x a a a --?+??+?? =112ln (ln )a a x a a a x a x a x ax a a a a --+?+??+?．

例20 若()x ?'存在，2(sec )arcsin y x x ?=+．求dy ．

分析 可以先求出dy dx

，也可利用微分的形式不变性求一阶微分． 解法1 dy

dx =22(sec )(sec )x x ?''=222(sec )sec tan x x x ?'?，

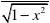
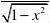
所以

dy =22

[2(sec )sec tan x x x dx ?'?．

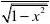
解法2 dy =2[(sec )arcsin ]d x x ?+=2(sec )arcsin d x d x ?+=22

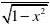
(sec )sec x d x ?' =22

[2(sec )sec tan x x x dx ?'?+．

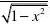
例21 设(cos )cos2f x x '=．求()f x ''． 解法1 在(cos )cos2f x x '=的两边微分，得

(cos )cos 2sin 2f x d x xdx ''=-，

即

(cos )(sin )4sin cos f x x dx x xdx ''?-=-，

化简得

(cos )4cos f x x ''=．

令cos x t =，则()4f t t ''=．于是可得

()4f x x ''=，||1x ≤．

解法2 由于

2(cos )cos22cos 1f x x x '==-，

于是

2()21f x x '=-，其中||1x ≤．

所以()4f x x ''=，||1x ≤．

注 本题作变换cos t x =，则要求||1t ≤．故在最后需指明{|11}x x -≤≤是()f x ''的定义域．

例22 设2sin ()y f x =且f 有二阶导数．求22d y dx ． 解 y '=22cos ()()2f x f x x '??=222()cos ()x f x f x '??，

y ''=22222()cos ()2()2cos ()f x f x x f x x f x '''?+???2222()[sin ()]()2x f x f x f x x ''+??-?? =2222222222()cos ()4()cos ()4[()]sin ()f x f x x f x f x x f x f x ''''?+??-??． 例23 已知函数()f x 具有任意阶导数且2()[()]f x f x '=．则当n 为大于2的正整数时()()n f x 是（ ）．

A ．1[()]n n f x +?．

B ．1![()]n n f x +?．

C ．2[()]n f x ．

D ．2![()]n n f x ?． 分析 已知2()[()]f x f x '=．应求出()f x ''，(3)()f x ，L ．用数学归纳法推出n 阶导数．

解 当2n ≥时，2()[()]f x f x '=，()f x ''=2()()f x f x '?=32[()]f x ?，以及

(3)()f x =223[()]()f x f x '???=4123[()]f x ???=43![()]f x ?，L ，

()()n f x =(1)![()]n n f x '-?=1![()]'()n n f x f x -??=1![()]n n f x +?．故选B ．

例24 设32()3||f x x x x =+，则使()(0)n f 存在的最高阶数n 为（ ）．

A ．0．

B ．1．

C ．2．

D ．3．

解 逐阶计算导数来验证，记

31()3f x x =，易见()1(0)n f 都存在，再记

22()||f x x x =，则由求导公式和定义，有

323 0() 0x x f x x x ?≥?=?-<??，，，2223, 0 ()3, 0x x f x x x ?≥?'=?-<??，26, 0()6, 0x x f x x x ≥?''=?-<?, 即2()6||f x x ''=，则有22

(0)(0)0f f '''==．由||x 在0x =不可导，知(3)2(0)f 不再存在，即2n =，选C ．

例25 设2sin y x =．求(100)(0)y ．

分析 求函数的高阶导数一般先求一阶导数，再求二阶，三阶，．．．，找出n 阶导数的规律，然后用数学归纳法加以证明．或者是通过恒等变形或者变量代换，将要求高阶导数的函数转换成一些高阶导数公式已知的函数或者是一些容易求高阶导数的形式．用这种方法要求记住内容提要中所给出的一些常见函数的高阶导数公式．

解法1 y =2sin x =11cos222

x -．则 sin 2y x '=， 2cos2y x ''=，

(3)22sin 2y x =-?， (4)32cos 2y x =-?，

(5)42sin 2y x =?，L ， (100)992cos 2y x =-?，

故(100)(0)y =992-．

解法2 利用公式()(sin )n kx =sin()2

n k k kx π?+．由2sin cos sin 2y x x x '==，得 (100)()y x =99992sin(2)2

x π?+， 故(100)(0)y =992-．

解法3 利用幂级数展开式()0()!n n f x a n =?．

2sin y x ==11cos222x -=210011111[12(2)(2)]222!4!100!

x x x --+-+-+L L L ， 故(100)(0)y =992-．

注 解法3用到了幂级数展开式，这是第十章无穷级数的内容． 例26 设2ln(32)y x x =-+．求(50)y ．

分析 先求出22332

x y x x -'=-+，若继续求导，将很难归纳出n 阶导数的表达式．此类有理分式函数，常常是将其分解为部分分式之和，再使用已有的公式．

解 由于223113212x y x x x x -'=

=+-+--，则 (50)y =(49)(49)11()()12x x +--=49495050(1)49!(1)49!(1)(2)x x -?-?+--=505049!49!(1)(2)x x ----．

例27 设函数()y y x =由方程cos()0x y e xy ++=确定，求.dy dx

分析 由方程(,)0F x y =确定的隐函数的求导通常有两种方法，一是只需将方程中的y 看作中间变量，在(,)0F x y =两边同时对x 求导，然后将y '解出即可；二是利用微分形式不变性，方程两边对变量求微分，解出dy ，则dx 前的函数即为所求．

解法1 在方程两边同时对x 求导，有

(1)sin()()0x y e y xy y xy +''+-+=，

所以

sin()sin()

x y

x y y xy e y e x xy ++-'=-． 解法2 在方程cos()0x y e xy ++=两边求微分，得

cos()0x y de d xy ++=，

即()sin()()0x y e dx dy xy xdy ydx ++-+=，从而sin()sin()

x y

x y y xy e dy dx e x xy ++-=-，所以 sin()sin()

x y

x y y xy e y e x xy ++-'=-． 例28 设函数()y f x =由方程1xy y xe =+所确定．求0|x y ='，0|x y =''．

解 将0x =代入方程1xy y xe =+，得1y =．先求0|x y ='，下面用两种解法求

0|x y ='．

解法1 对方程两边关于x 求导，可得

()xy xy y e x e y xy ''=+??+．

将0x =，1y =代入上式中可求得0|1x y ='=．

解法2 对方程两边关于x 微分得

即2xy xy xy dy x e dy xye dx e dx =++．化简得2(1)1xy xy dy e xy dx x e +=-．将0x =，1y =代入上式中求得

0|1x y ='=．

下面求y ''．对等式()xy xy y e x e y xy ''=+??+两边关于x 求导，得

y ''=2()()()()xy xy xy xy e y xy e y xy xe y xy xe y y xy '''''''++++++++，

将0x =，1y =，0|1x y ='=代入上式解得0|2x y =''=．

注 求y ''时，也可将等式2(1)1xy xy

e xy y x e +'=-两边对x 求导求得，或利用对数求导法．请读者自行完成这两种方法，并比较一下孰优孰劣．

例29 设函数()y y x =是由方程()f y y x e e ?=所确定，其中()f x 具有二阶导数且()1f x '≠．求22d y dx ．

解法1 对方程()f y y x e e ?=两边关于x 求导，得

()()()f y f y y e x e f y y e y '''+???=?，

即y '=()

()()f y y f y e e xe f y '-?=1()y y y e x e e f y ?'-?=1[1()]x f y '-，上式两端再对x 求导得 y ''=221{1()[()]}[1()]f y x f y y x f y ''''-?-+-?'-=2

23()[1()][1()]f y f y x f y '''--'-．

解法2 方程()f y y x e e ?=两端取对数得

ln ()x f y y +=，

对其两端关于x 求导则有

1()f y y y x '''+?=，

解得y '=1[1()]x f y '-．以下同解法1．

注 利用原方程简化导数表达式是隐函数求导常用的方法之一，在求隐函数的高阶导数时尤其显得重要．

例30 求函数()1x x y x =+的导数dy dx

． 分析 所给函数为幂指函数，无求导公式可套用．求导方法一般有两种：对数求导法和利用恒等式ln x x e =（0x >），将幂指函数化为指数函数．

解法1 对数求导法． 对等式()1x x y x

=+两边取自然对数得 ln [ln ln(1)]y x x x =-+，

两边对x 求导得

111[ln ln(1)]()1y x x x y x x

'?=-++-+， 解得

1()(ln )111x x x y x x x

'=?++++． 解法2 利用恒等式ln x x e =，（0x >）．

ln()[ln ln(1)]1()1x x x x x x x x y e e x

?-++===+． 于是

y '=[ln ln(1)]{[ln ln(1)]}x x x e x x x ?-+'??-+ =1()(ln )111x x x x x x

?++++． 注 一般的可导幂指函数()()v x y u x =均可采用上述两种方法求导． 例31 求由方程(cos )(sin )y x x y =所确定的函数()y x 的导数dy dx

． 分析 此题为幂指函数和隐函数求导数的综合问题．

解法1 对方程(cos )(sin )y x x y =两边取自然对数得

lncos lnsin y x x y =，

两端对x 求导，则有

sin cos ln cos lnsin cos sin x y y x y y x y x y

-''?+?=+??， 解得

lnsin tan ln cos cot dy y y x dx x x y +=-．

解法2 原方程可变为ln cos lnsin y x x y e e =，即

lncos lnsin y x x y =．

对上式两边微分：

即lncos lncos lnsin lnsin xdy yd x ydx xd y +=+， 于是有sin cos ln cos lnsin cos sin y x x y xdy dx ydx dy x y

-=+，由此解得 lnsin tan ln cos cot dy y y x dx x x y +=-．

例32 求函数y =的导数．

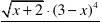
分析 该题属于求多个函数的乘积或幂的导数，用对数求导法较好． 解法1 两端先取绝对值，再取对数得

1ln ||ln(2)4ln |3|5ln |1|2

y x x x =++--+， 两边对x 求导，得

11452(2)31

y y x x x '?=--+-+．

所以145()2(2)31

y x x x '=--+-+．

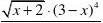
解法2 y ==1452(2)(3)(1)x x x -+?-+

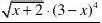
y '=14521(2)(3)(1)2

x x x --+?-+13524(2)(3)(1)x x x --+?-+14625(2)(3)(1)x x x --+?-+

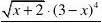
145()2(2)31x x x --+-+． 例33 设21cos x t y t

?=+?=?，则22d y dx =________． 分析 这是要求由参数方程确定函数的二阶导数，需要先求一阶导数．